Induced homomorphism (algebraic topology)

In mathematics, especially in the area of topology known as algebraic topology, an induced homomorphism is a way of relating the algebraic invariants of topological spaces which are already related by a continuous function.^[1] Such homomorphism exist whenever the algebraic invariants are functorial. For example, they exist for fundamental groups, higher homotopy groups, singular homology, and De Rham cohomology. For the more categorical approach, see induced homomorphism, and for the specific case of fundamental groups, see induced homomorphism (fundamental group).

Definitions

A continuous function 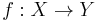$f:X\to Y$ between topological spaces (possibly with some additional structure) induces homomorphisms between various algebraic structures associated with $X$ and $Y$ , respectively.

Examples

A useful example is the induced homomorphism of fundamental groups. Likewise there are induced homomorphisms of higher homotopy groups and homology groups.

Any homology theory comes with induced homomorphisms. For instance, simplicial homology, singular homology, and Borel-Moore homology all have induced homomorphisms. Similarly, any cohomology comes induced homomorphisms. For instance, Čech cohomology, de Rham cohomology, and singular cohomology all have induced homomorphisms. Generalizations such as cobordism also have induced homomorphisms.

References

^ Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press. ISBN 0-521-79540-0. http://www.math.cornell.edu/~hatcher/AT/ATpage.html.